My friend did some really cool GPU optimization work over the summer. While he was explaining it to me, I realized there's a ton of really neat stuff here that I didn't understand. So I did some reading to nuance my understanding and am writing this post to reinforce what I learned.

I'm aiming to provide a somewhat high-level, but useful mental model of how GPUs work, how they are programmed, and the central issues with making GPU programs fast. I'll be focusing on NVIDIA GPUs.

What is a GPU

There are roughly two parts of a computer that might do computation (and can be programmed): the Central Processing Unit (CPU), and the Graphical Processing Unit (GPU).

"Graphical" is in the name because these chips were first developed to perform the types of computations abundant in graphics (vector operations), but those types of computations are also super important when doing scientific computing or training neural networks. Since ~2007, (NVIDIA) GPUs have been designed so that they can be used for applications beyond graphics.

Guts of a GPU

Somewhat like a CPU can contain multiple cores, GPUs contain multiple units called Streaming Multiprocessors (SMs); this is where the actual computation happens. An A100—a high-end NVIDIA GPU released in 2020—has 108 SMs.

Continuing with the "CPU-core" analogy, an SM has Arithmetic Logic Units (ALUs) inside, as well as registers, and memory caches. An SM differs in that there are many more ALUs, and that things are a lot more flexible.

We can view a GPU as a collection of SMs plus a pool of Global Memory shared by the SMs. Global Memory is also called High-Bandwidth Memory (HBM). This is the "GPU memory" that people talk about, and is the source of CUDA OOM errors.

Here's a diagram of an SM (sourced from the H100 whitepaper): That looks complicated, but let's break it down.

Compute Units

  • int32, fp32, fp64 units (CUDA Cores): While they're called CUDA Cores, they don't have their own registers or caches like a CPU core does, they are simply Arithmetic Logic Units (ALUs) that can perform operations on their respective data types.
  • The massive Tensor Cores are compute units that perform one algorithm only and do it really well: matrix multiplication. These were added by NVIDIA in 2017, and make up the majority of actual Floating Point Operations per second (FLOP/s) on a GPU these days.
  • The Special Function Unit (SFU) is the final bit that performs computation and is used to evaluate "special" functions like sin, cos, etc.

Registers and Memory

  • The Register File is a big block o' 32-bit registers. Unlike with a CPU, there is no concept of certain registers belonging to a particular core or compute unit. We'll get to how these are allocated/used in a moment.
  • The Shared Memory (SMEM) is a block of memory accessible within this SM. It's much faster to access than the GPU's global memory, so a lot of optimizations boil down to grabbing all the important data from Global Memory once, storing it in Shared Memory, and then doing all the relevant computation.
  • The Load/Store (LD/ST) units handle loading memory to/from the SM's Shared Memory, Register File, and the GPU's Global Memory.

Misc.

  • Finally the Tex units are specialized units for graphics textures that I'm going to ignore in this post.
  • GPU instructions are loaded into the Instruction Caches. I'm not going to talk about this really, as I don't think it's important to the high-level model I'm trying to paint.

What is a GPU Thread?

I've left out Warp Schedulers and Dispatch Units, because to understand them, we'll need to talk about the concept of "threads" in a GPU.

When writing a program for a CPU, our high-level program will eventually become a series of instructions (ex. add esp, 24h) that are executed one-at-a-time by a core 1. Similarly, GPU programs always compile to a list of instructions, but follow a Single-Instruction, Multiple Thread (SIMT) model, which means that multiple threads of execution will execute the same instruction simultaneously on different bits of data. This is similar to SIMD execution in CPUs (and TPUs), but a little more general, as we'll see later.

The Dispatch Unit is the bit of hardware that "issues" an instruction to a group of threads.

We call the threads executing the same set of instructions simultaneously a Warp. In practice, Warps contain 32 threads. When a Warp starts executing, registers are allocated from the Register File for each of its threads. These registers are reserved throughout the lifetime of that Warp.

Putting it all together: a series of instructions goes into a GPU, where it kicks off the start of a Warp composed of 32 GPU threads. Registers are allocated for each thread corresponding to how much they need, and the threads are issued instructions from the instruction list in lockstep by the Dispatch Unit, which the threads execute by using the different compute units, LD/ST units, etc.

Threads are able to perform distinct computation because each thread's index within a warp—called a lane—is baked into the hardware and available as a value in GPU instructions. For example, if we wanted our program to add two vectors, we could have each thread perform an add instruction using its lane as a memory offset into the vectors we're operating on. As you might imagine, it gets a little more complicated in practice as we often care about working with vectors/matrices that aren't of shape $1\times 32$, but this is a good model for now.

SIMT vs. SIMD

But wait, if all threads in a Warp are issued the same instruction for each clock cycle, does that mean I can't have any control flow? In a Single-Instruction, Multiple Data (SIMD) scheme, this would indeed be the case, but in the Single-Instruction, Multiple Thread (SIMT) scheme, control flow is enabled by allowing certain threads in the warp to be masked out. Imagine a series of instructions where some of the threads go down one execution path, and the rest go down another. When the instructions in the first path are being issued, the threads that want to run the other path are masked out, leading them to ignore the instructions in that block. When the other block is being run, the mask is flipped. See the figure below for a visual representation of this. 2

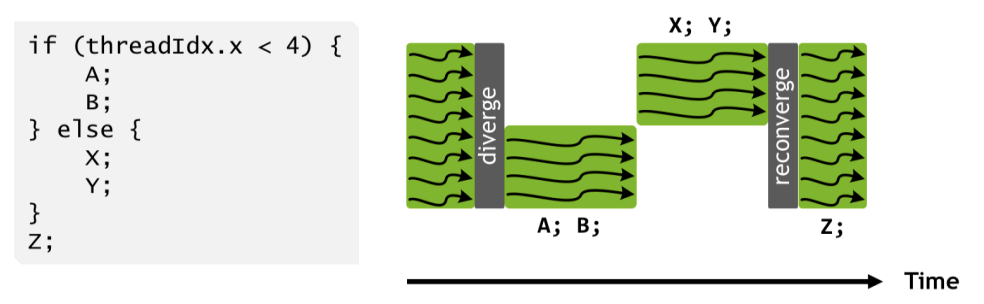
Zooming out another layer, GPUs are able to have many Warps "resident" on an SM, even though the number that can run at any time is bounded by the number of Warp Schedulers.

So is the number of warps an SM can have limited by the number of Dispatch Units it has? Kind of, but not quite. The number of warps that are running at once is indeed limited by the number of Dispatch Units, but an SM can hold many more warps than it can run in parallel. We call warps on an SM "resident". warps can be resident to an SM even if they're not running right now. A warp becomes resident to an SM when its instructions are first loaded onto the SM and registers and Shared Memory are allocated for its threads. When the warp finishes executing, that's all cleaned up and the warp is retired.

Having more resident warps than dispatch units is enabled by the Warp Schedulers. At the beginning of each clock cycle, each warp scheduler looks at all of the Warps resident on a GPU and chooses one to make progress on.

In fact, it's common for SMs to have hundreds of warps resident. This is a trick that GPUs use to get a high amount of concurrency on top of the parallelism 3 they exhibit. If one warp is waiting for a read from Global Memory to complete (which can take hundreds of clock cycles), a Warp Scheduler can immediately swap in another Warp for the next clock cycle. This allows GPUs to hide the latency of memory accesses to some degree.

How are GPUs programmed?

So that's a whirlwind tour of how each of the bits in a GPU work, but how do you actually program one?

At the lowest level, GPUs run instructions specified in Streaming Assembly (SASS). Different GPU architectures have different flavors of SASS, so there is a virtual assembly language called Parallel Thread Execution (PTX) that compiles to particular versions of SASS and allows some level of architecture-independent programming.

Instead of writing PTX, most people write in higher-level languages that compile to PTX. Popular languages are the CUDA C++ extension (often just called CUDA) and Triton. I'm going to talk about CUDA today, as it's lower-level and somewhat foundational.

CUDA code is an extension to C/C++ by NVIDIA to allow the writing of kernels, which are procedures that run on the GPU.

Here's a simple CUDA kernel that implements a matrix multiplication between two matrices, $A\in\mathbb{R}^{M \times K}$ and $B\in \mathbb{R}^{K\times N}$ to produce $C \in \mathbb{R}^{M \times N}$.

__global__ void matmul(int M, int N, int K, const float *A,
                            const float *B, float *C) {
    int i = blockIdx.y * blockDim.y + threadIdx.y;
    int j = blockIdx.x * blockDim.x + threadIdx.x;

    if (i >= M || j >= N) return;

    float sum = 0.0f;
    for (int k = 0; k < K; k++){
        sum += A[i * K + k] * B[k * N + j];
    }
    C[i * N + j] = sum;
}

Kernel definitions must start with a __global__ directive. Kernels are written as void functions that take pointers to Device Memory (what GPU programmers call a GPU's Global Memory/HBM). The kernel then accesses and mutates this data directly directly.

CUDA kernels are written from the perspective of a single thread. Each thread computes and writes a single entry in the result matrix: $C_{ij}=A_{i:} \cdot B_{:j}$.

But how do we get i and j?

Earlier I said GPU threads know which bits of data to act upon because each thread in a warp knows its lane (index within the warp). Of course, it's useful to be able to do more sophisticated things than a 0-31 index. This is where thread blocks and thread grids come in.

Thread blocks are a logical abstraction over GPU threads that allow programmers to work with groups of threads without thinking about warps. To make it easy to split up work between threads, thread blocks can be defined as a 1D, 2D, or 3D grid. Thread grids are a collection of thread blocks. They can also be 1D, 2D, or 3D.

In this diagram, we have blocks of $4 \times 4$ threads, and with a grid of $2 \times 2$ blocks, we're able to compute a matmul resulting in an $8 \times 8$ matrix. As you'll see below, we'll invoke our matmul kernel similarly, but with thread blocks of $16 \times 16$ threads, and a variable dimension thread grid that accounts for different matrix sizes.

The abstraction of thread blocks is realized via groups of one or more warps on the same SM at runtime. Because they're guaranteed to be on the same SM, threads within a thread block can access the same bit of Shared Memory.

Thread blocks can be put on different SMs, so they're not allowed to access the same Shared Memory.

To set up and run the kernel, we make use of this bit of code:

// alloc matrices in Host (CPU) Memory
int M = 1000, N = 500, K = 2000;
float* A = init_matrix(M, K);
float* B = init_matrix(K, N);
float* C = init_matrix(M, N);

// alloc + copy matrices to Device (GPU) Memory
float *d_A, *d_B, *d_C;
cudaMalloc(&d_A, sizeof(float) * M * K);
cudaMalloc(&d_B, sizeof(float) * K * N);
cudaMalloc(&d_C, sizeof(float) * M * N);

cudaMemcpy(d_A, A, sizeof(float) * M * K, cudaMemcpyHostToDevice);
cudaMemcpy(d_B, B, sizeof(float) * K * N, cudaMemcpyHostToDevice);

// define thread grid/blocks
dim3 block(16, 16);
dim3 grid((N + block.x - 1) / block.x, (M + block.y - 1) / block.y);

// launch kernel
matmul<<<grid, block>>>(M, N, K, d_A, d_B, d_C);
cudaError_t err = cudaGetLastError(); // check launch
if (err != cudaSuccess) {
	printf("Kernel launch failed: %s\n", cudaGetErrorString(err));
	exit(1);
}

// wait for warps to finish
err = cudaDeviceSynchronize();
if (err != cudaSuccess) {
	printf("Device sync failed: %s\n", cudaGetErrorString(err));
	exit(1);
}

// copy result from Device Memory
cudaMemcpy(C, d_C, sizeof(float) * M * N, cudaMemcpyDeviceToHost);
// Use result here...

We make use of cudaMalloc and cudaMemcpy to allocate and fill Device Memory with our matrices, declare the block and grid dimensions we want, and then invoke the kernel with the funky kernel_name<<<grid, block>>>(...) syntax. Finally we do some error checking and call cudaDeviceSynchronize, which will block until all the warps finish executing.

Note that this kernel is not using Shared Memory; each memory access A[..], B[...], and C[...] is loading/storing directly from/to HBM.

If we create a matmul.cu file with that kernel and invocation code, we can compile it with NVIDIA's nvcc compiler. I'm using an NVIDIA Titan RTX, which has a compute capability of 7.5, so I need to specify that in the flags:

$ nvcc -gencode arch=compute_75,code=sm_75 matmul.cu -o matmul
$ ./matmul
Latency: 1979 microseconds

How to make GPU programs fast?

If you're lucky enough to have an expensive GPU (or ten thousand of them), you'll want to make sure you're getting your money's worth and that your algorithms are utilizing the hardware's ability to perform useful FLOPs as much as possible. Optimization and performance is a hot topic because optimized implementations of algorithms can be orders of magnitude faster than naive implementations.

We can time our kernel against a CPU matmul algorithm:

void matmul_cpu( int M, int N, int K, const float* A, const float* B, float* C){
	for (int i = 0; i < M; ++i) {
		for (int j = 0; j < N; ++j) {
			float s = 0.0f;
			for (int k = 0; k < K; ++k) s += A[i*K + k] * B[k*N + j];
			C[i*N + j] = s;
		}
	}
}

and see that it gives us a pretty good speedup with matrices of this size:

GPU Latency: 2310 microseconds
CPU Latency: 6230041 microseconds

But is this the best our GPU can give us? A principled approach that performance engineers use here is to compute a roofline—the fastest a computation could theoretically run on a GPU—using the GPU's compute and memory specs. Then we could compare our performance to theoretical performance, and figure out whether our kernel is compute-bound, bottlenecked by the time it takes to perform computations, or memory-bound, bottlenecked by the time it takes to read from memory (typically Global Memory, or from the network if we're in a distributed GPU setup).

I'm just going to tell you that our naive kernel is extremely memory-bound. The compute bandwidth of GPUs is typically significantly greater than their memory bandwidth (read this post for a more nuanced understanding). In our kernel, essentially all of the computation and memory accesses are happening on this line:

sum += A[i * K + k] * B[k * N + j];

In this line, we're fetching two values from Global Memory, and performing a multiplication and an addition, so we have roughly one memory access per FLOP. Each read from Global Memory can take hundreds of clock cycles to complete, so we're spending almost the entire execution time waiting for bytes to be pulled in from Global Memory.

To figure out how to improve this, let's think about what bits of memory a single thread is accessing. Over the lifetime of a thread, it'll fetch a row from $A$ and a column from $B$ to compute its single entry in $C$: But the thread that's computing the entry one to the right also needs that row from $A$ and will be performing a lot of redundant work pulling it from Global Memory also! When you scale this redundant work across all of the threads, you realize we're making a lot of unnecessary accesses of Global Memory. 4

This leads us to an optimization. We can have the threads collaborate to pull the memory required into Shared Memory at the beginning, and then perform computations by accessing the values in Shared Memory. Because the matrices could be quite large, we can't load the entirety of $A$ and $B$ into Shared Memory at once, but we can have each thread block cooperate to load a tile from $A$ and a tile from $B$ at a time. The outer loop iterates over tiles of $A$ and $B$ and the inner loop computes the partial dot product over those tiles. Iterations in the outer loop are visualized in the figure below.

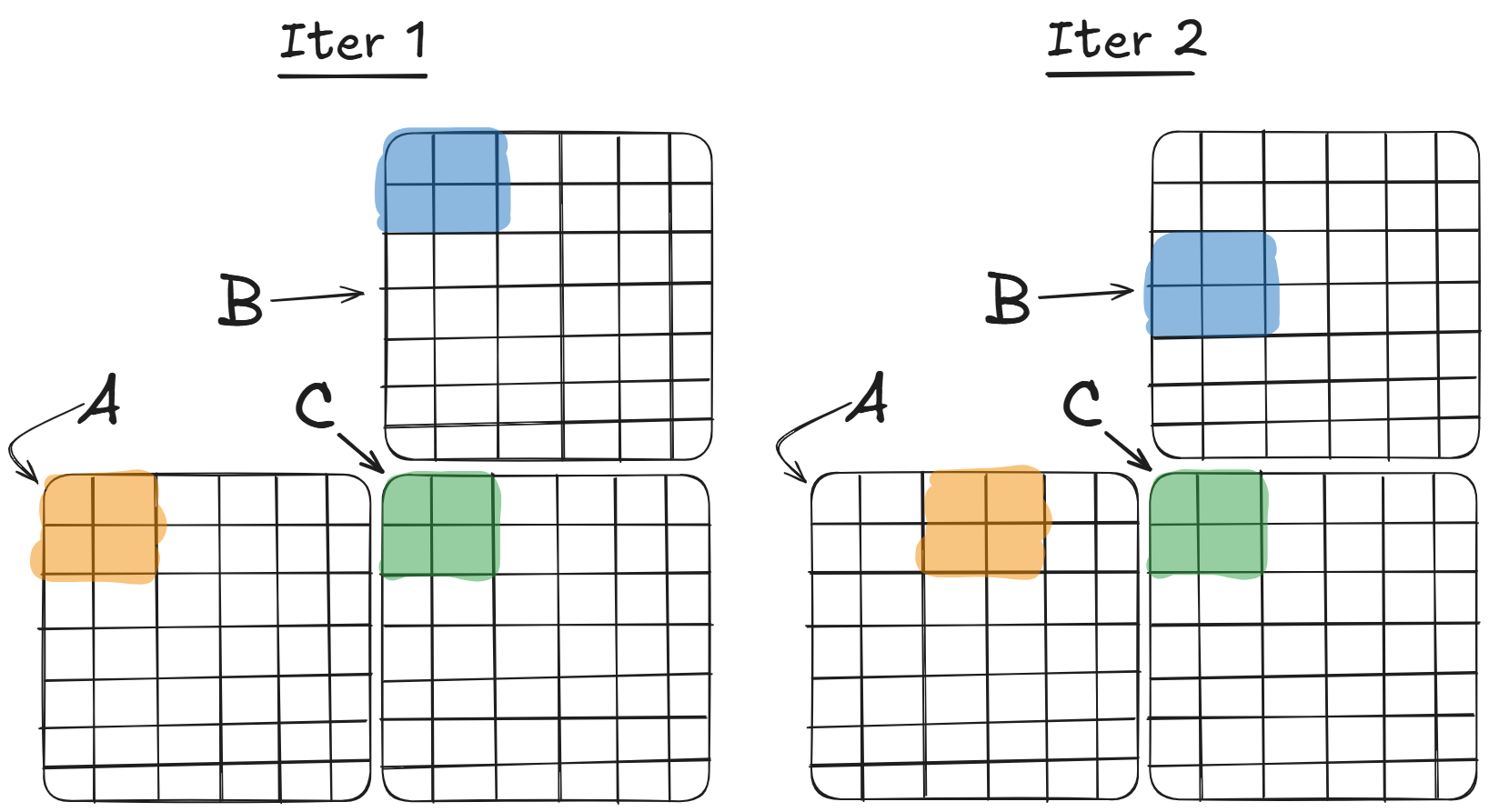
Here's an implementation of that algorithm. I have it here for completeness, but the important bits are:

  • we use the two __shared__ float A_tile[TILE_SIZE][TILE_SIZE] directives to tell the CUDA compiler each of our thread blocks wants two TILE_SIZE by TILE_SIZE blocks of shared memory. These will store our tiles of $A$ and $B$.
  • Each thread now cooperates to fill A_tile and B_tile before using them to aggregate the next slice of the dot product. In one iteration of the for loop, each thread will fetch one entry from $A$ and $B$ into A_tile and B_tile. Assuming we launch with a thread grid of TILE_SIZE $\times$ TILE_SIZE, this means A_tile and B_tile will be fully populated.
  • Because our thread blocks contain more than 32 threads, they'll be composed of multiple warps, which will execute at potentially different times. We use the __syncthreads() primitive to block until all warps in a block have reached that line of execution. 
#define TILE_SIZE 16

__global__ void matmul_tiled(int M, int N, int K, const float *A,
                             const float *B, float *C) {
    // Allocate shared memory for tiles
    __shared__ float A_tile[TILE_SIZE][TILE_SIZE];
    __shared__ float B_tile[TILE_SIZE][TILE_SIZE];
            
    // Each thread computes one element of the C matrix
    int row = blockIdx.y * TILE_SIZE + threadIdx.y;
    int col = blockIdx.x * TILE_SIZE + threadIdx.x;
    
    float sum = 0.0f;    
    // Loop over tiles of A and B to compute C element
    for (int tileIdx = 0; tileIdx < (K + TILE_SIZE - 1) / TILE_SIZE; ++tileIdx) {
        // Load tile of A into shared memory
        int aRow = row;
        int aCol = tileIdx * TILE_SIZE + threadIdx.x;
        if (aRow < M && aCol < K) {
            A_tile[threadIdx.y][threadIdx.x] = A[aRow * K + aCol];
        } else {
	        // load 0 if we're beyond the edge of A
            A_tile[threadIdx.y][threadIdx.x] = 0.0f;
        }
        
        // Load tile of B into shared memory
        int bRow = tileIdx * TILE_SIZE + threadIdx.y;
        int bCol = col;
        if (bRow < K && bCol < N) {
            B_tile[threadIdx.y][threadIdx.x] = B[bRow * N + bCol];
        } else {
	        // load 0 if we're beyond the edge of B
            B_tile[threadIdx.y][threadIdx.x] = 0.0f;
        }
        
        // Synchronize to ensure tiles are fully loaded
        __syncthreads();
        
        // Perform dot product on current tiles
        for (int k = 0; k < TILE_SIZE; ++k) {
            sum += A_tile[threadIdx.y][k] * B_tile[k][threadIdx.x];
        }
        
        // Synchronize before loading next tiles
        __syncthreads();
    }
    
    // Write result to global memory
    if (row < M && col < N) {
        C[row * N + col] = sum;
    }
}

This way, the memory accesses of $A$ and $B$ are shared within a thread block. Does this give us a material speed up?

Naive GPU Latency: 2316 microseconds
Tiled GPU Latency: 1460 microseconds

Yup! The speedup is only around 50% because of cache hits in the naive case giving us some of this benefit for free.

Sum-Up and Pointers to Resources

That's a lot of information, but here's a high-level picture that I think is a good takeaway:

  • GPUs are made of a bunch of units called Streaming Multiprocessors. Each contains a bunch of flexible compute (ALUs/Tensor Cores) and memory/registers.
  • GPU threads use this compute to act on the memory/registers in groups: warps at the hardware level, which get aggregated into thread blocks and thread grids.
    • GPUs employ a Single-Instruction Multiple-Thread paradigm, where each thread in a group will receive the same instruction, but act on different pieces of data.
  • Writing optimized kernels is an art, and often comes down to reducing the amount of global memory/network accesses you need so that your GPU can spend more of its time performing computations.

Here are various pointers for the interested:

Thanks to Alex Portland and Julian Beaudry for feedback

1

or at least in a fashion that simulates serial execution

2

More deets: SIMT allows arbitrary control flow via a stack of masks. When it hits a point with divergence, it pushes a mask onto the stack for each possible path, and then continues to serially pop/execute each mask.

3

Remember, concurrency $\neq$ parallelism. Parallelism is when things are literally running at the same time, and concurrency is a weaker version where we can swap threads of execution to give the appearance of things running at the same time. Concurrency is often useful to speed IO-bound operations, as we can go work on other stuff while ex. a memory access is executed.

4

We're being somewhat saved by the L1 Caches here, as they're saving accesses from Global Memory to be used again. However they're not perfect, and we're still leaving a lot on the table.